Die Aufgabe setzt ein paar Geometriekenntnisse voraus.

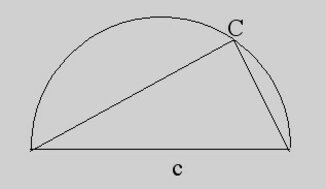
1) Der Satz des Thales: Zeichne eine Strecke c und den Halbkreis, der c als Durchmesser hat.
Zeichne ein Dreieck, das c als Grundseite hat und dessen dritte Ecke C auf dem Halbkreis liegt. Dann ist der Winkel in C ein rechter.

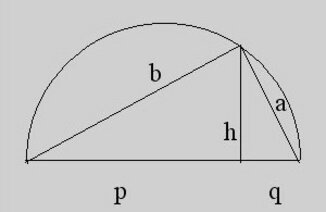
2) Satz des Pythagoras: Das Hypotenusenquadrat ist gleich der Summe der beiden Kathetenquadrate : c² = a² + b²

Und eine Folge davon:h² = pq( h die Höhe auf der Hypotenuse, p,q die Teilstrecken der Hypotenuse, die sich als Folge der Teilung durch h ergeben ( p + q = c)

Noch ein Hinweis, der zur folgenden Aufgabe zwar nicht benötigt wird, hier aber nicht schaden kann. Das arithmetische Mittel aus p und q ist der Radius des Halbkreises: (p+q)/2 = c/2 . Das geometrische Mittel aus p und q ist die Höhe h ( sie ist die Wurzel aus dem Produkt pq). h kann höchstens gleich dem Radius sein; das ist dann der Fall, wenn p=q=c/2 . Das arithmetische Mittel zweier Größen p und q ist also größer oder gleich dem geometrischen Mittel; es ist diesem gleich im Fall p = q

Berechnung der "ersten kosmischen Geschwindigkeit" ( Idee und Zeichnung entnommen aus den Feynman-lectures)

Nach dem sog. Unabhängigkeitsprinzip ist im Erdschwerefeld die Bewegung eines Körpers unabhängig davon, wie er sich zugleich in waagerechter Richtung bewegt; er führt in senkrechter Richtung stets einen freien Fall aus. Wenn man zwei Körper zugleich in Bewegung setzt, wobei man den ersten einfach frei fallen lässt, den zweiten aber mit einem kräftigen Schwung in waagerechter Richtung in Bewegung setzt, so kommen beide im gleichen Augenblick auf dem Boden auf.

Das Experiment kann nur so lange in dieser Weise ausgehen, wie die Erkrümmung sich noch nicht bemerkbar macht.

Ein frei fallender Körper legt in der ersten Sekunde des Fallens eine Strecke von 5 m zurück. 

Wie weit muss er sich in dieser Sekunde in waagerechter Richtung bewegen, um seine Lage relativ zum Erdboden nicht zu verändern ?

Er muss sich in einer Sekunde genau so weit in waagerechter Richtung bewegen, dass sich der Erdboden unter ihm um 5 m nach unten weggebogen hat. Wie weit ist das?

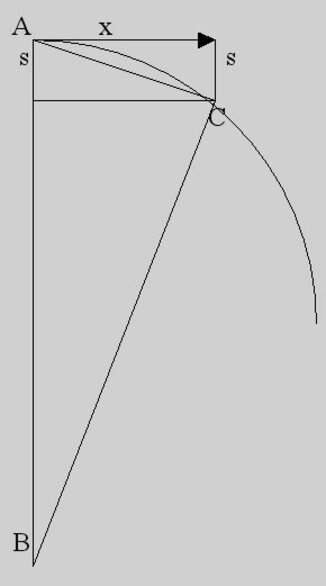
In der – grob unmaßstäblichen Zeichnung – bedeuten x die gesuchte Strecke , s = 5m die Fallstrecke, AB = 2R = 12752km den Erddurchmesser. Der Bogen deutet die Erdkrümmung an.

In C liegt gemäß dem Satz des Thales ein rechter Winkel vor, x ist Höhe in dem rechtwinkligen Dreieck ABC. Der Höhensatz ergibt x² = (2R – s)s, also in sehr guter Näherung x² = 2Rs = = 12752•0,005 km² und damit x = 7,98 km.

Das ergibt einen ausgezeichneten Näherungswert für die sog. erste kosmische Geschwindigkeit; das ist eben die Geschwindigkeit, mit der sich ein Satellit bewegt, der in nur geringer Höhe über der Erdoberfläche umläuft ( „gering“ gemessen am Erdradius R).

Sie beträgt etwa 7,93 km/sec und wird gewöhnlich mit dem Ansatz v²/R = g berechnet.

Gegenüber der formelmäßigen Standard-Rechnung erscheint mir die Feynman’sche Herangehensweise sehr anschaulich und direkt; übrigens ist es doch ein wenig erstaunlich, dass sich die Erdoberfläche bereits nach weniger als 10 km um mehr als 5 m weggekrümmt hat ( man denkt an die oft zitierte Beobachtung einer Annäherung eines Schiffes an die Küste)

Oder ganz anschaulich: Fahre mit der Saarbahn vom Landwehrplatz bis Brebach. Dann hat sich die Erde bereits um eine Zimmerhöhe weggekrümmt.

Zu Richard Feynman

Er hat gelebt von 1918 bis 1988. Nobelpreis in Physik 1965 für einige seiner Beiträge zur Kernphysik. Von 1950 bis zu seinem Tod am California Institute of Technology in Pasadena tätig. In den sechziger Jahren hielt er eine Anfängervorlesung in Physik, die als Feynman lectures veröffentlicht worden ist und die als eine der besten Lehrveranstaltungen gilt, die je im Fach Physik gehalten worden ist. Unbestritten der originellste akademische Lehrer der Physik im letzten Jahrhundert. Der Nobelpreisträger Feynman war sich nicht zu schade, mit seinen Studenten die wichtigsten Rechentricks des elementaren Integrierens zu üben oder ihnen eine Einführung in die Entstehung der Logarithmentafeln zu geben. In seinen letzten Lebensjahren entscheidend an der Aufklärung des Challenger-Unglücks von 1986 beteiligt.