Wir beweisen den genannten Satz.

Seien u, v zwei natürliche Zahlen, und seien u₁₁ und v₁₁ deren Elferreste. Dann gibt es zwei natürliche Zahlen a und b mit u = a•11 + u₁₁ und v = b•11 + v₁₁

Damit gilt. u•v = (a•11 + u₁₁)( b•11 + v₁₁) = a•b•11•11 + a•v₁₁•11 + u₁₁•b•11 + u₁₁•v_{11<o:p></o:p>}

Die Produkte uv und u₁₁v₁₁ unterscheiden sich nur um ein Vielfaches von 11; sie haben deshalb denselben Elferrest. Dieser Satz ist ein mächtiges Hilfsmittel, da das zweite Produkt sehr viel kleiner als das erste sein kann.

Die ersten beiden Wertepaare haben wir schon: (1 | 7) und ( 2 | 5)

7³ = 7²7¹ ; demnach hat 7³ denselben Elferrest wie 5•7 = 35, und der ist 2.

7⁴ = 7³7¹; der Elferrest von 7⁴ ist gleich dem von 2•7, und der ist 3.

7⁵ = 7⁴7¹; der Elferrest von 7⁵ ist gleich dem von 3•7, und der ist 10

7⁸ = (7⁴)²; der Elferrest von 7⁸ ist gleich dem von 3², und der ist 9

7¹² = (7⁴)³; der Elferrest von 7¹² ist gleich dem von 3³, und der ist 5

7¹⁶ = (7⁸)² ; der Elferrest von 7¹⁶ ist gleich dem von 9², und der ist 4

7¹⁹ = 7³7⁴7¹²; der Elferrest von 7¹⁹ ist gleich dem von 2•3•5=30, und der ist 8

7³² = (7¹²)²•7⁸; der gesuchte Elferrest ist gleich dem von 5²•9, der wiederum gleich dem von 3•9, und der ist 5.

Und jetzt ein bisschen fachsprachlich korrekt: 7³⁸=7¹⁹7¹⁹ ≡ 64mod11 ≡ 9mod11

Das Zeichen a ≡ bmod11 heißt "a ist kongruent b modulo 11" und bedeutet, dass die zwei Zahlen a und b denselben Elferrest haben.

Und 7⁷⁶ hat denselben Elferrest wie 81, und der ist 4.

Das Zahlenpaar (16| 4) habe ich an den Schluss gestellt, um auf etwas sehr Wichtiges aufmerksam zu machen: Unsere Funktion ist nicht injektiv, d.h. verschiedene x- Werte können denselben y-Wert haben. Und das bedeutet, dass die Funktion nicht umkehrbar ist!

Es gibt sogar unendlich viele x-Werte, welche den y-Wert 4 haben, und Gleiches gilt für alle Elemente des Wertebereiches! Damit ist es unmöglich, aus einem gegebenen y-Wert den zugrunde gelegten x-Wert zu erraten!! Das wird sich später als entscheidend herausstellen.

Und wenn Du jetzt das folgende Schema verstehst, dann ist die Aufgabe Singh 2 nur noch ein kleiner Spaziergang.

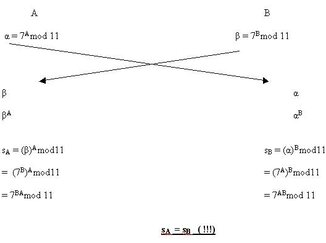
Gegeben sind zwei natürliche Zahlen A und B. Die Elferreste von 7^A und 7^B bezeichnen wir mit α bzw. β

Was geschieht, wenn wir jetzt β^A und α^B bilden und dann deren Elferreste bestimmen?

Eine kleine Erläuterung dazu: β ist der Elferrest von 7^B. Und so hat die Potenz β^A denselben Elferrest wie (7^B)^A ; Entsprechendes gilt für α, den Elferrest von 7^A

Beachte bitte, dass A und B nicht die Seiten wechseln: A bleibt links, B bleibt rechts.