a)
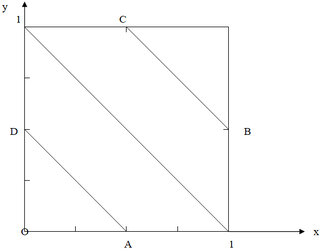
Das Quadrat mit den Eckpunkten O, (1|0), (1|1), (0|1) repräsentiert die Ergebnismenge
a1) Die zu a1) gehörenden Ergebnisse (x|y) erfüllen die Ungleichung x+y < 1 oder y< - x + 1 : Das Dreieck 0, (1|0), (0|1) repräsentiert diese Menge; es gilt daher p = ½
a2) Die Ergebnisse erfüllen die Ungleichung x + y < 3/2 ; Das Fünfeck mit den Eckpunkten
0, (1|0), B, C, (0|1) repräsentiert die Lösungsmenge; es gilt p = 1 – 0,5(0,5•0,5) = 7/8
a3) Die Punkte (x|y), welche die Ungleichung 0,5 < x+y < 3/2 erfüllen, liegen in dem Sechseck mit den Punkten D, A, (1|0), B, C, (0|1); es gilt daher p = 1 - 2•1/8 = ¾
( Das Dreieck 0AD hat ebenso wie das Dreieck B, (1|1), C den Inhalt 1/8 )
b1) Das geometrische Mittel zweier positiver Zahlen ist kleiner als das arithmetische Mittel (Gleichheit gilt nur, wenn die beiden Zahlen gleich sind). Wenn die Wahrscheinlichkeit, dass das arithmetische Mittel der Zufallszahlen kleiner als ½ ist, gleich ½ ist, dann liegt die Wahrscheinlichkeit, dass das geometrische Mittel kleiner als ½ ist, über ½.
Der Vollständigkeit halber hier noch der Beweis, dass das geometrische Mittel zweier voneinander verschiedener positiver Zahlen x,y kleiner als ihr arithmetisches Mittel ist.
(xy)0,5 < (x+y)/2 ↔ 4xy< (x+y)2↔ 4xy<x2 + 2xy + y2 ↔ 0 < x2 – 2xy + y2 = (x-y)2
b2)
Es muss gelten x•y <1/4 ↔ y < 1/(4x) und 0 < x,y<1 : Die Lösungsmenge wird repräsentiert im Bereich x = 0,25 bis x = 1 durch die Fläche unter der Hyperbel mit der Gleichung
y = 1/(4x) und im Bereich x = 0 bis x= 0,25 durch das Rechteck mit den Eckpunkten O, (0,25|0), (0,25|1), (0|1) . Der Inhalt der gesamten Fläche ist gleich dem Inhalt des Rechtecks (= 0,25) plus dem bestimmten Integral der Funktion 1/(4x) über dem Intervall (0,25|1), also gleich
0,25 + ¼ •( ln(1) – ln(1/4) ) = 0,25 – ¼ •ln(1/4) = 0,25 + 0,3465 = 0,5965
Die Wahrscheinlichkeit, dass das geometrische Mittel der Zufallszahlen x,y kleiner als ½ ist,
hat den Wert 0,5965