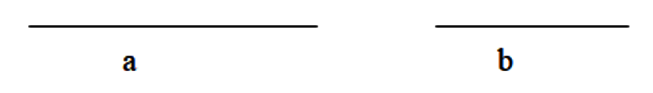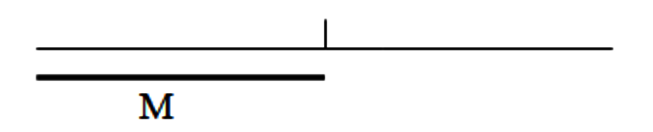1.1. Der Median ist 11,5 sec. Der Durchschnitt ist ( 10,1 + 22 + 11,5 + 11,6 + 23,4)/7 = 11,2
Von den gegebenen Werten liegt 11,0 in kleinster Entfernung vom Durchschnitt.
Offenbar zieht der extreme Wert 10,1 den Durchschnitt „zu sich heran“. Er fällt besonders stark ins Gewicht. Beim Median spielt er keine besondere Rolle. Das ist ein Vorteil des Median bzw. ein Nachteil des Durchschnitts. Andererseits lässt der Median nicht erkennen, dass ein extremer Wert vorhanden ist, da er diesen nicht heraushebt.
1.2. Seien t1, t2, t3, t4 die Zeiten der Staffelläufer über ihre jeweiligen 100 m. Der vierhundert Meter - Läufer muss in der Zeit t1 + t2 + t3 + t4 die Runde laufen, also: v = 400/( t1+t2+t3+t4)
Daraus folgt v = 400/( 100/v1 + 100/v2 + 100/v3 + 100/v4) = 4/(1/v1 + 1/v2 + 1/v3 + 1/v4)
2) Silkes Punktzahl nach dem 1. Jahr: 5500•1,12; nach dem 2. Jahr: 5500•1,12•1,15,
nach dem 3. Jahr: 5500•1,12•1,15•1; dem 4. Jahr: 5500•1,12•1,15•1•1,
dem 5. Jahr 5500•1,12•1,15•1•1•0,75; schließlich nach dem 6. Jahr ( im siebenten Wettkampf) 5500•1,12•1,15•1•1•0,75•0,98 = 5500•0,9467 = 5207 .
Der mittlere Wachstumsfaktor sei x; es muss gelten: x6 = 0,9467 : Der mittlere Wachstumsfaktor ist das geometrische Mittel aus den einzelnen Wachstumsfaktoren. x ist die sechste Wurzel aus 0,9467; x = 0,99 .
Wenn Silke jedes Jahr ihre Leistung um 1% verringert hätte, wäre sie nach 6 Jahren ( im siebenten Wettkampf) bei der gleichen Leistung angekommen wie im tatsächlichen Verlauf.
Man kann sagen: Die mittlere prozentuale Änderung ist gleich -1 ( und keineswegs gleich Null: Die 12% und 15% Steigerung dürfen nicht einfach addiert und mit den prozentualen Verminderungen von 25% und 2% zu Null verrechnet werden! Das wäre ein Fehler: Mittlere Wachstumsfaktoren sind geometrische, nicht arithmetische Mittelwerte).
3) Führt man (1,3)•(3,5) (erst (3,5), dann (1,3)) aus, so steht danach Spielerin 1 auf Platz 3; führt man (3,5)•(1,3) aus, so steht danach Spielerin 1 auf Platz 5.
4) E = (8,9+9,1+9,06)/3= 9,02; σ2 = ((0,12)2+(0,08)2+(0,04)2)/3 und σ = 0,086. Die Streuung beträgt 8,6cm.
Einige Mittelwerte lassen sich gut geometrisch veranschaulichen.
Geometrische Deutung verschiedener Mittelwerte
Seien a, b positive Zahlen; sie werden durch zwei Strecken dargestellt.

Das arithmetische Mittel oder der Durchschnitt M = (a+b)/2

Das geometrische Mittel G = (a•b)1/2
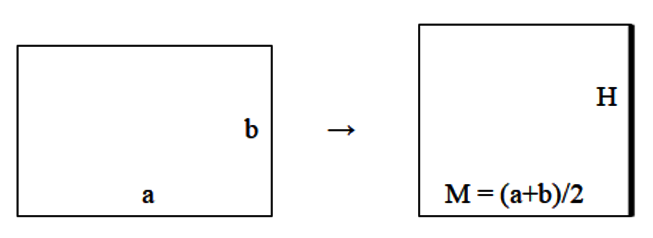
Verwandle ein Rechteck mit den Seitenlängen a, b in ein flächengleiches Quadrat. Dessen Seite ist das geometrische Mittel aus a und b.
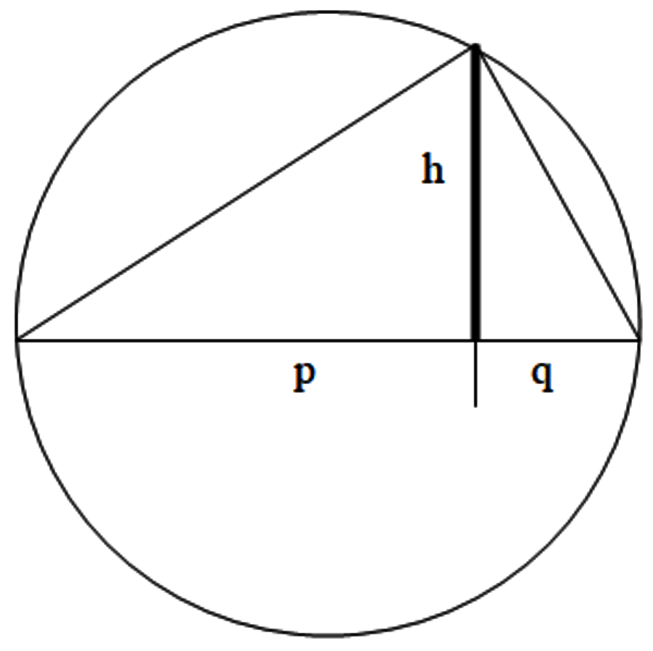
Nach dem Höhensatz ist im rechtwinkligen Dreieck h2 = p•q, wobei p,q die Teile der Hypotenuse sind, welche durch den Fußpunkte der Höhe geteilt wird.

Die dick eingetragene Höhe h ist das geometrische Mittel der beiden Hypotenusenabschnitte p und q. Die Katheten sind nur aus „dekorativen“ Gründen eingefügt worden.
Das harmonische Mittel H ist gegeben durch: 1/a + 1/b = 2/H
oder H = 2ab/(a+b) = ab/((a+b)/2)
Das Rechteck mit den Seiten a, b ist durch ein flächengleiches Rechteck zu ersetzen, dessen eine Seite gleich dem Durchschnitt aus a und b ist; seine andere Seite ist das harmonische Mittel H.

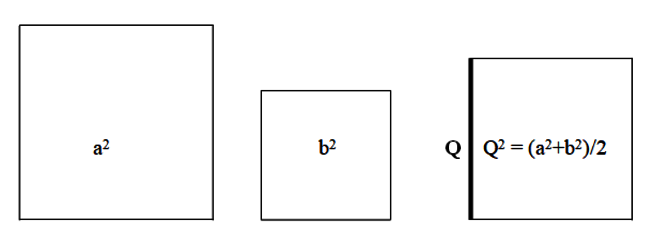
Das quadratische Mittel Q ist die Wurzel aus dem Durchschnitt der Quadrate von a und b:
Q = ( (a2 + b2)/2 )1/2 . Man bildet ein Quadrat, dessen Inhalt gleich dem Durchschnitt der Inhalte der Quadrate mit den Seitenlängen a und b ist. Dessen Seitenlänge ist das quadratische Mittel Q aus a und b.

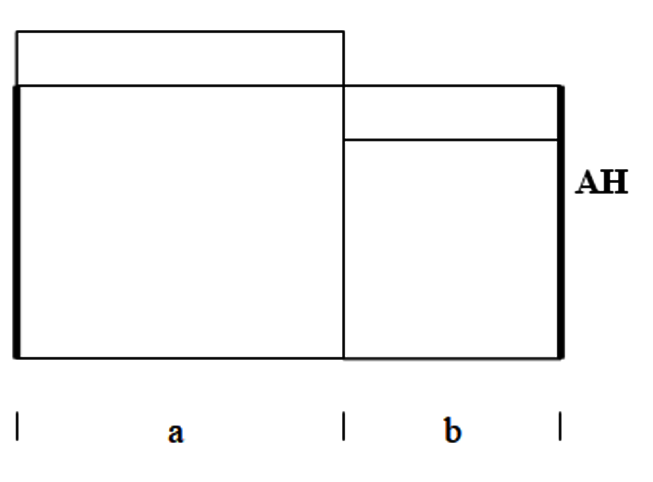
Das antiharmonische Mittel ist die Wurzel des Quotienten aus der Summe der Quadrate von a und b und der Summe aus a und b :
AH = ( (a2 + b2)/(a + b) )1/2 . Man fügt die beiden Quadrate a2 und b2 aneinander; es entsteht eine Grundseite der Länge (a + b). Diese bildet eine Seite eines Rechtecks, dessen Inhalt gleich der Summe der Inhalte der beiden Quadrate ist. Die andere Seite des Rechtecks ist das antiharmonische Mittel.