a)Der Winkel, unter dem die Torpfosten vom Elfmeterpunkt erscheinen, ist Peripheriewinkel eines Kreises, der die Torlinie als Sehne hat und auf dem der Elfmeterpunkt liegt. Weitere Sehnen dieses Kreises sind die Strecken, welche den Elfmeterpunkt mit den Torpfosten verbinden. Die Mittelsenkrechten auf diesen Sehnen schneiden sich im Mittelpunkt M des Kreises. Die Entfernung des Elfmeterpunktes vom Punkt M ist gleich dem Radius des Kreises.
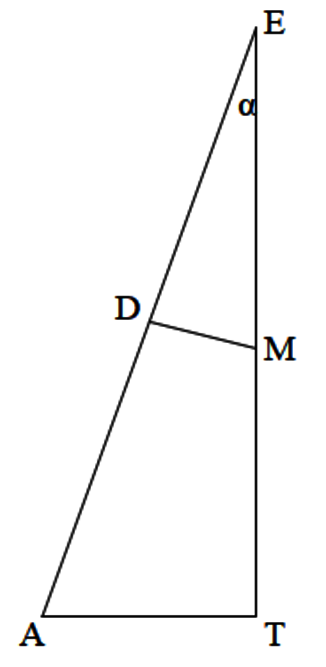
In der Skizze bezeichnen A einen Torpfosten, E den Elfmeterpunkt, T die Mitte der Torlinie, D die Mitte der Strecke AE.
Gegeben sind die Längen der Strecken AT ( = halbe Torpfostenentfernung = 3,66m), TE = 11m.
Der Winkel α ist gleich arctan(3,66/11) = 18,41° . Die Torpfosten erscheinen vom Elfmeterpunkt aus unter dem Winkel 36,82°.
AE ist Hypotenuse des rechtwinkligen Dreiecks ATE; seine Länge ist die Wurzel aus der Summe der Quadrate 3,662 + 112 ; man erhält 11,59 m . Die Länge der Strecke DM errechnet sich aus |DM| = |ED|•tan(18,41°) = (11,59m/2)•tan(18,41°) =1,93m . Die Strecke EM ist der gesuchte Radius; sie ist Hypotenuse im rechtwinkligen Dreieck DME; die Wurzel aus der Summe der Quadrate (11,59/2)2 + 1,932 ist gleich 6,1.
Die Punkte, von denen aus die Torlinie unter dem gleichen Winkel erscheint wie vom Elfmeterpunkt aus, liegen alle auf dem Kreis mit dem Radius 6,1m und dem Mittelpunkt M, der von der Mitte der Torlinie aus in Richtung Elfmeterpunkt in 4,9m Entfernung liegt ( das ist nahezu auf der Fünfmeterlinie).
b) s = 47,14 und α = 3,57 .
Man bildet die „Abweichungs“ - Vektoren αD und sD mit den Komponenten αDi = αi –α bzw. sDi = si –s ; i = 1,...,7 .
Es ist αD = (21,43|-13,57|16,43|6,43|-18,57|-3,57|-8,57)
und sD = (2,86|-7,14|12,86|7,86|-12,14|12,86|-17,14)
Die Streuung erhält man aus σα = ( ( αD12 + αD22 + ...+αD72)/7 )0,5 = 14,06 und entsprechend aus den Komponenten von sD die Streuung σS = 11,3
Die Streuung wurde hier direkt aus ihrer Definition berechnet. In den Rechnern ist gewöhnlich der Weg über die Verschiebungsformel vorgesehen; der Aufwand wäre im hier gegebenen Fall bei beiden Wegen jedoch ungefähr gleich groß.
Der Korrelationskoeffizient ist der Quotient aus dem Skalarprodukt αD•sD = Σ αDi· sDi =746,43
und dem Produkt der Beträge dieser Vektoren: |αD| = ( αD12 + αD22 + ...+αD72)0,5 = 37,23 ,
sowie |sD| = 29,88 .
Also: r = 746,43/(37,23· 29,88) = 0,67
Freilich liefern die Taschenrechner meist diese Werte „auf Knopfdruck“ ohne dass man sich damit befasst, wie die Rechner zu Werke gehen. Es kann vorkommen, dass ein Rechner unaufgefordert eine Stichprobe der Werte vornimmt, z.B. den größten und kleinsten Wert weglässt, so dass kleinere Abweichungen von den hier kalkulierten exakten Werten möglich sind. Es stimmt unbehaglich, wenn der Rechner eine Voraussetzung seiner Kalkulation verschweigt: Die Gleichwahrscheinlichkeit der Messwerte. Das Weglassen „verdächtiger“ Werte hilft der Erfüllung dieser Voraussetzung nach.
Der Korrelationskoeffizient ist ein Kosinus: Es ist der Kosinus des Winkels, den die beiden
Abweichungsvektoren einschließen. Der schwankt zwischen 1 ( die beiden Vektoren sind parallel) und – 1 ( die beiden Vektoren sind antiparallel). Ein Wert von 0,67 besagt, dass die beiden Größen die Tendenz haben, sich in die gleiche Richtung zu ändern, was in unserem Fall bedeutet, dass die weiten Abschläge dazu tendieren, nach links zu gehen. Das heißt natürlich nicht, dass die Weite die Richtung beeinflusst. Im vorliegenden Fall könnte ein Seitenwind von rechts wehen, oder auch der Torwart könnte mit dem rechten Fuß schießen; in solchen Fällen driftet der Ball nach links ab.
