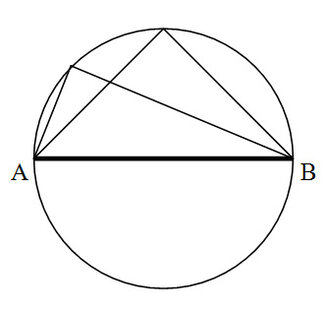
a) Die Punkte, von denen aus eine Strecke AB unter einem rechten Winkel erscheint, bilden den Thaleskreis. Wie immer die Begrenzung liegt, der Punkt C liegt auf dem Halbkreis mit dem Durchmesser AB . Der Inhalt des Dreiecks ABC ist maximal, wenn C genau senkrecht über dem Mittelpunkt des Thaleskreises liegt. Dann ist das Dreieck gleichschenklig; die Winkel in A und B sind gleich 45°, und das Dreieck hat den Inhalt 1/2•(AB •AB/2) = 1 m²

b)

Das gleichschenklige Dreieck mit der Basis AB und mit dem Spitzenwinkel γ – und damit den Basiswinkeln α =β = (180° - γ)/2 – ist eindeutig bestimmt. Peter kann seine Begrenzung in dieser Weise legen. Damit hat er auch schon das Dreieck mit maximalem Flächeninhalt abgegrenzt, wovon man sich wie folgt überzeugt. Alle Punkte, von denen aus die Strecke AB unter dem Winkel γ erscheint, liegen auf dem Umkreis um dieses Dreieck: γ ist Peripheriewinkel über der Sehne AB . Offensichtlich hat das gleichschenklige Dreieck als dasjenige mit dem größten Abstand des Punktes C von der Strecke AB und damit als dasjenige mit der größten Höhe den größten Flächeninhalt.

Der Inhalt des Dreiecks ABC ist gegeben durch 1/2• AB • h = 1/2• AB • (( AB /2)•tan(α)) =

= ( (AB )² /4 ) • tan(α)

Im Fall γ = 40° und AB = 2m ist α = 70° , und der Inhalt ist gleich 2,75m²

Ein Hinweis zum Verfahren, das bei der Lösung hier verwendet worden ist. Man wechselt das Bezugssystem ( einfacher ausgedrückt: den Standpunkt). Im beschriebenen Experiment liegt die Ecke C des Beetes fest, die begrenzende Strecke AB wird verschoben. Die Lösung wird aber recht einfach , wenn man die Sache von der Strecke aus sieht, diese als ruhend betrachtet und den Punkt C wandern lässt.