a) und b) .Die beiden Funktionen, die nach den Vorschriften gemäß a) und b) gebildet werden, sind in dem Intervall von 0 bis 1 streng monoton wachsend. Zu jeder der beiden Funktionen gibt es eine Zahl r aus [0;1], von der ab die Funktionswerte größer oder gleich 1 sind. Nach Voraussetzung ist das Maß der Wahrscheinlichkeit, dass die Zahl x in einem Teilintervall von [0;1] liegt, gleich der Länge dieses Teilintervalls. Der Erwartungswert E(g) des Gewinns des Spielers ist deshalb gegeben durch:
E(g) = r•( -2) + (1-r)•3 = -2r + 3 – 3r = 3 – 5r
Der Erwartungswert ist negativ, d.h. die Bank gewinnt auf lange Sicht, wenn r>0,6.
Zu zeigen ist demnach: In beiden Fällen a) und b) ist die Zahl x, von der ab die Funktionswerte größer oder gleich 1 sind, größer als 0,6.
Setzt man im Fall a) für x die Zahl 0,6 ein, so ergibt sich 0,96: d.h. die Zahl x, von der ab der Funktionswert größer oder gleich 1 ist, muss größer als 0,6 sein ( wer es ausrechnen möchte:
x2 + x = 1 hat im Intervall [0;1] die Lösung 50,5/2 – 0,5 ≈ 0,618) .
Im Fall b) erhält man: x3/2 + 0,5 ≥ 1 ↔ x3/2 ≥ 0,5 . Es folgt x ≥ 0,52/3 = 0,251/3
Die dritte Wurzel aus 0,25 ist größer als 0,6, wovon man sich direkt überzeugen kann,
da 0,63 = 0,36•0,6 = 0,216 < 0,25 bzw. 0,251/3 > 0,6
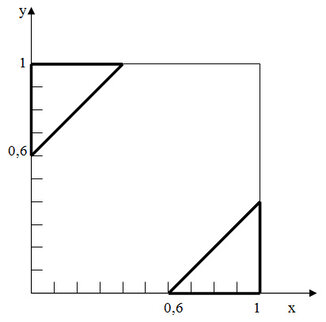
c) |x-y| > 0,6 → (x>y ^ x-y>0,6) v (x<y ^ y-x>0,6) → (x>y ^ y< x – 0,6) v (x<y ^ y>x+0,6)
In der folgenden Skizze ist die Lösungsmenge { (x|y) }dargestellt; es handelt sich um die beiden rechtwinkligen Dreiecke, die fett umrandet sind.

Der Inhalt der beiden Dreiecksflächen zusammen beträgt 2•1/2•0,42 = 0,16. Damit ist die Gewinnwahrscheinlichkeit gleich 0,16; die Wahrscheinlichkeit eines Verlustes ist gleich 0,84.
Der Erwartungswert des Gewinns errechnet sich zu 0,16•5 + 0,84•(-1) = - 0,04 < 0
Auf lange Sicht wird also die Bank gewinnen.