a) 2π•(R + ΔR) = 2π•R + 2π•ΔR . Es ist also ΔU = 2π•ΔR. Damit ist ΔR = ΔU/(2 π) .
Dieser Wert ist unabhängig von R; er beträgt im gegebenen Fall (5/π) cm . Das jeweilige zweite Seil, das um den Äquator bzw. den Pfeiler gelegt wird, verläuft um dieses Stück oberhalb der Erd-bzw. der Pfeileroberfläche.
Man kann die Aufgabe auch in folgender Weise angehen. Der durch die Änderung des Umfangs neu entstehende Kreis geht aus dem ursprünglichen durch eine zentrische Streckung hervor. Streckzentrum ist der Kreismittelpunkt, der Streckfaktor sei k. Um diesen Faktor ändern sich sowohl der Umfang als auch der Radius, und R/U ist eine Konstante. Wie bei jeder proportionalen Funktion sind die Quotienten ΔR/ΔU und R/U gleich; in diesem Fall ΔR/ΔU = R/U = 1/(2π) .
b) Wiederum kann man die Aufgabe durch den Hinweis auf die zentrische Streckung lösen. Das durch die Änderung des Umfangs entstehende gleichseitige n-Eck geht aus dem ursprünglichen durch eine zentrische Streckung hervor. Streckzentrum ist der Mittelpunkt des Inkreises; sowohl der Umfang des n-Ecks wie auch der Radius des Inkreises ändern sich um den gleichen Streckfaktor. Der Quotient R/U ist konstant; er ändert sich mit der Größe des n-Ecks nicht. Er ist gleich dem Quotienten ΔR/ΔU , der damit ebenfalls nicht von der Größe des n-Ecks abhängt.
Vielleicht hat der Leser eine weniger direkte Lösung gewählt; im folgenden wird eine solche Schritt-für-Schritt-Lösung angeboten. Dabei wird auch der Quotient R/U ausgerechnet ( zur Lösung der Aufgabe benötigt man diesen Wert nicht; es genügt zu wissen, dass er konstant ist).
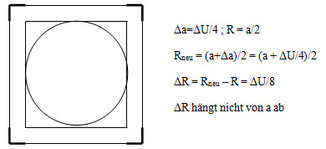
Sehen wir uns zunächst das Quadrat an, wo die Lösung recht anschaulich ist.

Im Fall des gleichseitigen Dreiecks kann man wie folgt rechnen.
Δa =ΔU/3 ; R = (1/3)•( 30,5•a)/2 = (30,5/6)•a ; Rneu = (30,5/6)•(a + ΔU/3) also ΔR = (30,5/18)•ΔU
Gehen wir nun zum allgemeinen Fall des gleichseitigen n-Eck.
Ein solches n-Eck lässt sich in n gleich große gleichschenklige Dreiecke zerlegen; deren Höhe ist gleich R, den Winkel an der Spitze bezeichnen wir mit γ ( γ = 2π/n) . Wir erhalten:
U = na; tan(γ/2) = tan(π/n) = a/(2R) → R = a/(2tan(π/n)) und R = U/(2n•tan(π/n))
R ist proportional zu U : ΔR = ΔU/(2n•tan(π/n))
In jedem gleichseitigen n- Eck ist also bei einer gegebenen Änderung des Umfangs die damit einhergehende Änderung des Radius des Inkreises nicht vom bisherigen Umfang bzw. nicht von der Seitenlänge a und damit nicht von der Ausdehnung („Größe“) des n-Ecks abhängig.
Die Gleichung ΔR = ΔU/(2n•tan(π/n)) geht übrigens im Fall, dass n über alle Grenzen wächst in die oben zum Kreis hergeleitete Gleichung ΔR = ΔU/(2π) über:
n•tan(π/n) = (n•sin(π/n))/cos(π/n) . Verwendet man die Reihenentwicklung von Sinus und Cosinus, so findet man, dass der Nenner gegen 1, der Zähler gegen π konvergiert.
